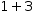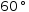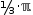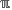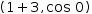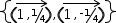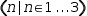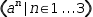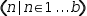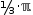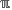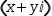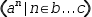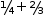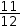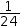2.3.3 Tangible and Manifest Values

The literal form of a number is an irreducible symbol that represents a unique numeric quantity. Myron classifies a number as a tangible value. Closely related to the idea of tangible value, a manifest expression is an expression that can be reduced to a tangible value, typically through simplification. In particular, a manifest expression can be an operator whose operands are either tangible or manifest. Examples are 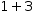1+3 and cos 0. Note that 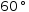60 ° is not tangible because it simplifies to 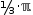1/3⋅ℼ and 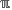ℼ is not tangible.

Tangibility also extends to composites and collections. Their literal form uses an n-ary notation to indicate contained expressions. They are tangible only if all of the contained expressions are also tangible and they are manifest only if the contained expressions are tangible or manifest. Examples are 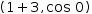(1+3, cos 0) and 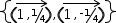{(1, 1/4)ɽ, (1, -1/4)ɽ}.

Composite and collection literals are irreducible in the sense that the number of contained expressions is fixed by the literal; such literals are always iterable. Collections can also be represented by generators. Collection generators are iterable if their domains are manifest; they are tangible if they are iterable and their templates are manifest. For example, 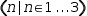(n|n∈1, 3) is tangible because the template is implicitly bound to the tangible expressions in the domain. However, 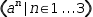(a^n|n∈1, 3) is not tangible because although it is iterable the template contains an unbound and hence non-manifest variable; 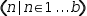(n|n∈1, b) is not iterable because the domain contains an unbound variable. An iterable generator can replaced by a collection literal using Distribute . An intangible iterable generator distributes to an intangible literal.

An intangible expression can become tangible upon successful binding. When this happens, an expression becomes evaluable. That is, while 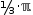1/3⋅ℼ is not tangible, it can be evaluated by binding 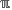ℼ to a numeric approximation. Similarly, when the intangible 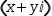(x, y)ⅈ is bound to tangible definitions for x and y, the expression is evaluable and hence tangible. Similarly, 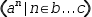(a^n|n∈b, c) becomes iterable when bound to tangible definitions of a, b and c.

Manifest expressions in the form of numeric fractions are retained in that form unless they simplify to an integer. On the one hand, 1/4 is the same tangible value as 0.25, but an expression like 1/4+2/3 displays as 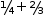1/4+2/3 and simplifies to 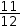11÷12 rather than 0.917. The actual numeric value is obtained by Evaluate . 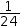Numbers that represent simple inverses, like 0.041666666666666664 can be transformed to a fraction equivalent 1÷24 using special simplification.